This problem to the AI4OPT challenge was suggested by prof. Ivan Oseledets
Problem
Let $ A\in\mathbb{R}^{n\times r} $ have orthonormal columns ($ A^\top A=I_r $). Does there always exist a set of $ r $ row indices $ S\subset {1,\dots,n} $ such that the square submatrix $ \widehat A:=A[{S,:}]\in\mathbb{R}^{r\times r} $ is invertible and
$$ |\widehat{A}^{-1}|_2 \le \sqrt{n} ? $$
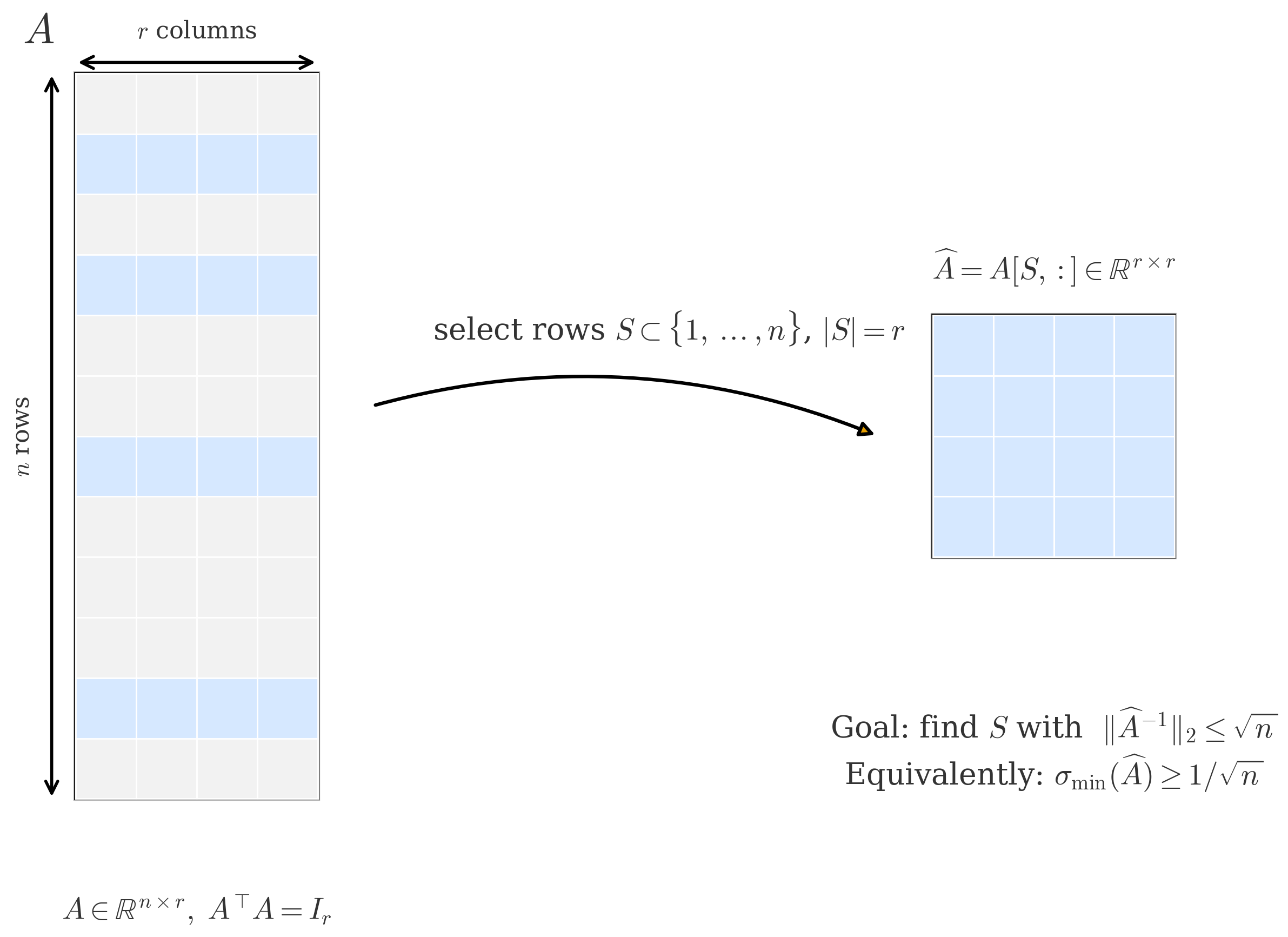
Equivalently, does there exist $ S $ with $ \sigma_{\min}(\widehat A)\ge 1/\sqrt{n} $? This is the formulation due to Goreinov-Tyrtyshnikov-Zamarashkin and is closely related to pseudoskeleton/CUR approximations. [1], [2]
Geometric reformulations
The statement is equivalent to:
- There exists a coordinate $ r $-subspace whose largest principal angle to $ \operatorname{range}(A) $ is at most $ \arccos(1/\sqrt{n}) $.
-
For every $ k $-circle in $ \mathbb{R}^n $ (the unit sphere in a $ k $-subspace), some orthogonal projection onto a coordinate $ k $-subspace stays outside the open ball of radius $ 1/\sqrt{n} $.
These equivalences are written explicitly in [2] (Formulations 2-4).
Status and known results
- Trivial base case $ r=1 $. Suppose, we have a matrix $ A \in \mathbb{R}^{n \times 1} $, therefore matrix $ A^TA = 1 $. In this case our matrix is just a vector $ a $. We need to prove, that for any vector $ a $ there is a choice of $ 1 $ index out of $ n $, such that $ a_i \geq 1/\sqrt{n} $. Assume it’s not possible, which means, that for any vector $ a $ all its coordinates $ a_i < 1/\sqrt{n} $, therefore, the maximum coordinate in this vector is also smaller, than $ 1/\sqrt{n} $, i.e. $ |a|2^2 = \sum{i=1}^n a_i^2 < n (\max_i a_i)^2 < n \frac{1}{n} < 1 $, which is obviuously, not true, since $ a^Ta = 1 $.
- Smallest nontrivial real case $ (n=4,r=2) $. Proved. For every real $ 4\times 2 $ semi‑orthogonal $ A $, there is a $ 2\times 2 $ submatrix with $ \sigma_{\min} \ge 1/2 $ (equivalently $ |\widehat A^{-1}|_2\le 2=\sqrt{4} $), and the bound is sharp; explicit equality cases are constructed. [2]
- General real case. Open for all $ 1< r < n-1 $ beyond $ (n=4,r=2) $. Numerical experiments suggest the $ \sqrt n $ bound, if true, is best possible. [3]
- Complex case (already for $ r=2 $). The real‑case $ \sqrt n $ estimate fails over $ \mathbb{C} $; Nesterenko gives a counterexample and recasts the problem via polygons in $ \mathbb{R}^3 $, proposing a different optimal constant $ B_n<1 $ in the principal‑angle formulation. [3]
References
- Y. Nesterenko. Submatrices with the best‑bounded inverses: revisiting the hypothesis. arXiv:2303.07492 (proof for (n=4,r=2); equivalent formulations and sharpness).
- Y. Nesterenko. Submatrices with the best‑bounded inverses: Studying (\mathbb{R}^{n\times 2}) and (\mathbb{C}^{n\times 2}). arXiv:2408.16631 (polygon‑space reformulation for (r=2); complex‑case counterexample).
- S. A. Goreinov, E. E. Tyrtyshnikov, N. L. Zamarashkin. A theory of pseudoskeleton approximations. Linear Algebra and Its Applications, 261 (1997), 1–21. (Origins of the hypothesis and the max‑volume viewpoint.) (ScienceDirect)
- J.-C. Hausmann, A. Knutson. Polygon spaces and Grassmannians. L’Enseignement Mathématique 43 (1997), 173–198. (Background used in the (r=2) reductions.) (Université de Genève)
- A. Naor. Restricted invertibility revisited. arXiv:1601.00948 (context on selecting large well‑conditioned submatrices/coordinates). (arXiv)
